Pythonで楕円状の点を求める

お久しぶりです。未経験エンジニアのいすいです。

最近Webサイトで要素をカッコよく配置したいなって時に、楕円状に並べたらカッコよくね！？って思い、要素を楕円状で等間隔に並べようと試みました。

そしたら、楕円状に並べるのって意外とむずい！😱

というのは、楕円って弧の長さ求めるのすごく大変みたいなんです。

楕円の公式
実践

楕円の公式

楕円の弧の長さは以下の公式になります。

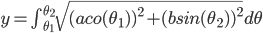
a:長半径、b:短半径

この積分は楕円積分と言って、既知の初等関数であらわすことが出来ないことがわかっています。つまり、これ以上簡単な式に直せないんです。

とはいえ積分をプログラミングでやると数値計算のアルゴリズムとか考えなくちゃいけなくて大変そう。。

うーん

どうしよ。。

と、ここで、pythonにはすごい便利なライブラリがあったことを思い出しました。

それがScipyです。

このscipyを使うと簡単に積分が解けちゃいます。🤪

（ぶっちゃけ最強です。）

というわけで、本日はpython(scipy)を用いて楕円状に物を配置するやり方をご紹介します。

実践

楕円の前提

楕円状に物を配置するとは？

ということに関してですが、以下のような図を想定しています。

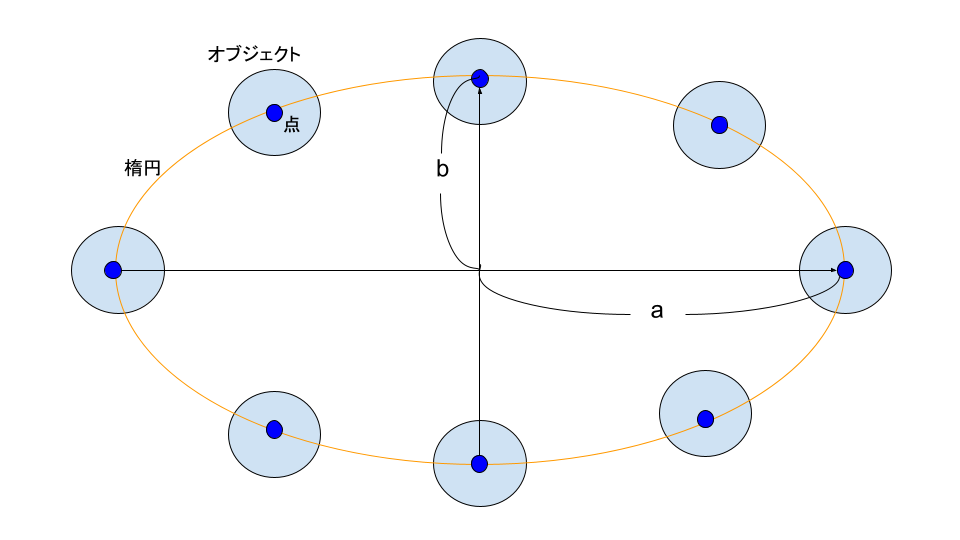
オレンジの線が楕円で、長半径a、短半径b

オブジェクト（今回は円を想定してますが、別にどんな形でもOKです。ただし、中心点は考える必要があります。）の中心点が楕円上にあるようにします。

正直オブジェクト自体（形、大きさ等）は重要ではなく、楕円上の等間隔の点の座標を求めることが今回の目的になります。

求めるもの

今回は、長半径a、短半径b、オブジェクト数nから

各オブジェクトの中心点の座標を求めます。

UIは触れないのかよ！と思われた方もいるかと思いますが、それは各々で好きなように反映させてください。🙇🏻‍♂️

得られた座標は一番上から半時計まわりに順番に並べたものになります。

ちなみに長半径と短半径は逆でも問題ありません。

座標は楕円の中心を原点(0,0)としています。シチュエーションに応じて左上を原点にしたりとカスタマイズしてください。

コード

あらかじめ scipy は pip でインストールしておいてください。

# NumPyをインポート
import numpy as np

# mathをインポート
import math

# SciPy積分パッケージをインポート
from scipy import integrate

# 長半径
A = 440

# 短半径
B = 290

# オブジェクトの個数
N = 10

# ０からradiamまでの弧の長さ取得
def getArcLengthDiff(radian1, radian2):
    # 関数を定義
    y = lambda x: np.sqrt((A * np.cos(x))**2 + (B * np.sin(x))**2)

    # yを0からpiまで数値積分
    integ = integrate.quad(y, radian1, radian2)

    return integ[0]

# 楕円一周分の長さ
L = getArcLengthDiff(0, 2* np.pi)

# オブジェクト間の距離
d = L / N

# 計算結果のラジアンリスト
radian_list = [np.pi/2]

# １つ前のラジアン（一番上スタート）
radian_prev = np.pi/2

# １周後のラジアン
radian_end = 5 * np.pi /2

# 一つ目のラジアン（一番上スタート）
r1 = np.pi/2

# ２つ目のラジアン
r2 = radian_end

for i in range(N-1):
    while(True):
        if r2 - r1 < math.pow(10, -10):
            radian_list.append(r2)
            radian_prev = r2
            r1 = r2
            r2 = radian_end
            break

        midium = r2 + (r1 - r2)/2
        arc = getArcLengthDiff(radian_prev, midium)
        if arc < d:
            r1 = midium
        else:
            r2 = midium

# 各オブジェクトの座標
location_list = []

for radiam in radian_list:
    location_list.append((A*math.cos(radiam)+450, 300-B*math.sin(radiam)))

print([(int(l[0]),int(l[1])) for l in location_list])

コード解説

まず最初に長半径a、短半径b、オブジェクト数nを設定してください。

実行するとint型にパースされた座標（x,y)のリストが出力されると思います。

コードの処理の流れは以下です。

scipyを用いて、弧の長さを求める関数を定義

↓

長半径a、短半径bから楕円の一周の長さ取得

↓

１周の長さをオブジェクトの個数nで割って、オブジェクト間の距離を計算

↓

２分探索を用いて、オブジェクト間距離になるラジアンを計算　
✖️(かける) オブジェクト個数

↓

求めたラジアンから座標を取得

以上となります。

Pythonで楕円状の点を求める

楕円の公式